Traffic flow prediction is of great significance for urban planning and alleviating traffic congestion. Due to the randomness and high volatility of urban road network short-term traffic flow, it is difficult for a single model to accurately estimate traffic flow and travel time. In order to obtain more ideal prediction accuracy, a combined prediction model based on wavelet decomposition and reconstruction (WDR) and the extreme gradient boosting (XGBoost) model is developed in this paper. Firstly, the Mallat algorithm is applied to perform multi-scale wavelet decomposition on the average travel time series of the original traffic data, and single branch reconstruction is performed on the components at each scale. Secondly, XGBoost is used to predict each reconstructed single-branch sequence, so as to obtain multiple sub-models, and the Bayesian algorithm is used to optimize the hyperparameters of the sub-models. Finally, the algebraic sum of the predicted values of all sub-models is used to obtain the overall traffic prediction result. To test the performance of the proposed model, actual traffic flow data has been collected from a certain link of the Brooklyn area in New York, USA. The performance of proposed WDR-XGBoost model has been compared with other existing machine learning models, e.g., support vector regression model (SVR) and single XGBoost model. Experimental findings demonstrated that the proposed WDR-XGBoost model performs better on multiple evaluation indicators and has significantly outperformed the other models in terms of accuracy and stability.
| Published in | International Journal of Transportation Engineering and Technology (Volume 10, Issue 1) |
| DOI | 10.11648/j.ijtet.20241001.12 |
| Page(s) | 15-24 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Traffic Time Prediction, Wavelet Analysis, XGBoost, Bayesian Algorithm
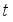 refers to the real-time predicting of traffic characteristics in the next time
refers to the real-time predicting of traffic characteristics in the next time 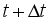 even later, and the predictive time-span is not more than 15 minutes or less than 5 minutes. Generally, predicting is based on three basic parameters of macroscopic traffic flow: average traffic volume, average speed and average occupancy, average travel time et al. Those are the traffic characteristics from the perspective of the whole transportation system. In contrast, there are few studies regarding the average travel time of the link as the predicting result. Thus, the average travel time of the link refers to the average travel time of all vehicles through the observation link during a certain time interval, as shown in formula (1):
even later, and the predictive time-span is not more than 15 minutes or less than 5 minutes. Generally, predicting is based on three basic parameters of macroscopic traffic flow: average traffic volume, average speed and average occupancy, average travel time et al. Those are the traffic characteristics from the perspective of the whole transportation system. In contrast, there are few studies regarding the average travel time of the link as the predicting result. Thus, the average travel time of the link refers to the average travel time of all vehicles through the observation link during a certain time interval, as shown in formula (1): 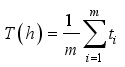 (1)
(1) 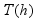 is the average link travel time in the
is the average link travel time in the 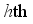 time interval,
time interval, 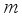 is the total number of vehicles passing through the link during the observation interval,
is the total number of vehicles passing through the link during the observation interval, 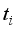 is the travel time of the
is the travel time of the 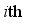 vehicle through this link. Considering that the current road condition is related to the road condition in the past intervals, the average travel time in the past several intervals is used to forecast the average travel time in the future interval. Specifically, the average travel time
vehicle through this link. Considering that the current road condition is related to the road condition in the past intervals, the average travel time in the past several intervals is used to forecast the average travel time in the future interval. Specifically, the average travel time 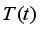 of the
of the 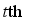 time interval on the target link can be described as a time series as follow:
time interval on the target link can be described as a time series as follow: 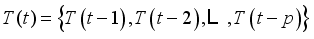 (2)
(2) 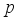 is the time lag.
is the time lag. 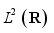 , the function
, the function 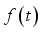 is expanded by a wavelet function, which is called continuous wavelet transform (CWT), and the expression is
is expanded by a wavelet function, which is called continuous wavelet transform (CWT), and the expression is 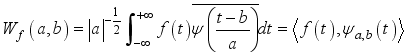 (3)
(3) 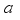 is the scaling factor and
is the scaling factor and 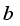 is the translation factor;
is the translation factor; 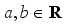 and
and 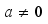 .
. 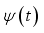 is basic wavelet;
is basic wavelet; 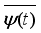 is the conjugate function;
is the conjugate function; 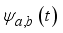 is a family of functions generated by scaling and translation of basic wavelet, which is called wavelet function.
is a family of functions generated by scaling and translation of basic wavelet, which is called wavelet function. 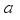 and translation factor
and translation factor 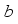 , namely
, namely 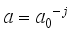 ,
, 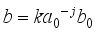 (4)
(4) 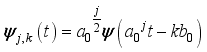 (5)
(5) 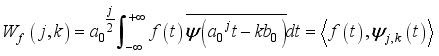 (6)
(6) 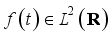 can be expressed as a wavelet series
can be expressed as a wavelet series 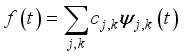 (7)
(7) 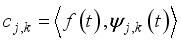 is called wavelet coefficients.
is called wavelet coefficients. 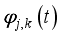 and wavelet function
and wavelet function 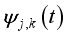 , and the corresponding decomposition coefficient sequence
, and the corresponding decomposition coefficient sequence 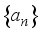 ,
, 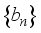 to reconstruct the coefficient sequence
to reconstruct the coefficient sequence 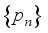 ,
, 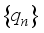 . The original traffic flow data can be decomposed into low-frequency approximate component
. The original traffic flow data can be decomposed into low-frequency approximate component 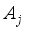 and high-frequency detail component
and high-frequency detail component 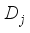 at a certain scale
at a certain scale 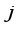 by low-pass filter and high-pass filter, namely
by low-pass filter and high-pass filter, namely 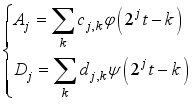 (8)
(8) 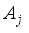 can be further decomposed as
can be further decomposed as 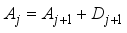 (9)
(9) 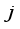 -scale decomposition is performed, the formula is as follows:
-scale decomposition is performed, the formula is as follows: 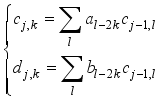 (10)
(10) 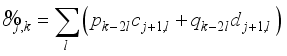 (11)
(11) 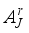 and the detail components
and the detail components 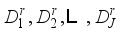 can be obtained. Finally, approximate component and all detail components are algebraically added, and the reconstructed series is
can be obtained. Finally, approximate component and all detail components are algebraically added, and the reconstructed series is 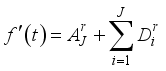 (12)
(12) 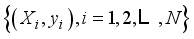 ,
, 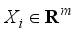 is the eigenvector of
is the eigenvector of 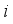 th instance and
th instance and 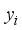 is the attribute value of
is the attribute value of 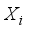 . XGBoost model is defined as the following addition model, and its base classifiers are classification and regression tree (CART):
. XGBoost model is defined as the following addition model, and its base classifiers are classification and regression tree (CART): 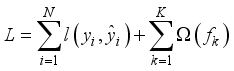 (13)
(13) 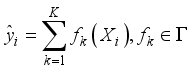 (14)
(14) 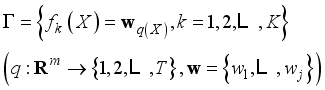 (15)
(15) 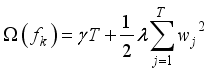 (16)
(16) 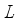 is the optimization function of XGBoost model and
is the optimization function of XGBoost model and 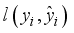 is the error function between the forecasting value
is the error function between the forecasting value 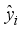 and the actual value
and the actual value 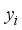 corresponding to
corresponding to 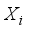 ;
; 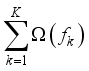 is the sum of the complexity of all
is the sum of the complexity of all 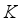 trees, which is added to the objective function as a regularization term to effectively prevent over fitting;
trees, which is added to the objective function as a regularization term to effectively prevent over fitting; 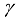 and
and 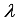 are regularization parameters.
are regularization parameters. 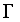 is a set of CART.
is a set of CART. 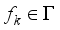 is a tree model which means mapping a eigenvector of instance to the corresponding a leaf node;
is a tree model which means mapping a eigenvector of instance to the corresponding a leaf node; 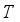 is the number of leaf nodes of tree;
is the number of leaf nodes of tree; 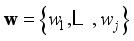 represents the weight vector of all leaf nodes of a tree.
represents the weight vector of all leaf nodes of a tree. 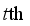 step, the second-order Taylor expansion of the objective function is carried out, and the expression is as follow:
step, the second-order Taylor expansion of the objective function is carried out, and the expression is as follow: 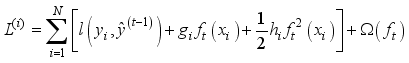 (17)
(17) 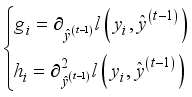 (18)
(18)  steps in equation (17), let
steps in equation (17), let 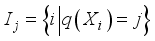 be the set of all samples belonging to the
be the set of all samples belonging to the 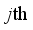 leaf node. By minimizing this formula, the optimal weight
leaf node. By minimizing this formula, the optimal weight 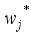 of the
of the 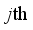 leaf node of the
leaf node of the 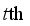 sub-model and the corresponding optimal objective function value can be obtained by:
sub-model and the corresponding optimal objective function value can be obtained by: 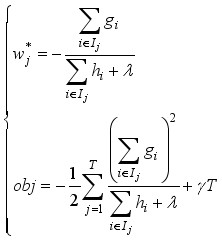 (19)
(19) 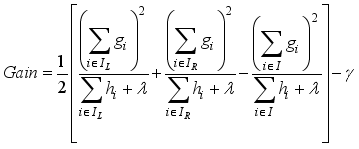 (20)
(20) 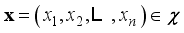 , and the objective function
, and the objective function 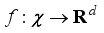 is a black box with no analytics and higher evaluation cost. The optimal value satisfying the following equation (21) needs to be found:
is a black box with no analytics and higher evaluation cost. The optimal value satisfying the following equation (21) needs to be found: 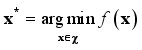 (21)
(21) 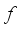 , parameter search space
, parameter search space 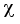 , surrogate function
, surrogate function 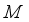 , acquisition function
, acquisition function 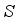 , number of iterations
, number of iterations 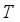 . Then the algorithm steps can be expressed as:
. Then the algorithm steps can be expressed as: 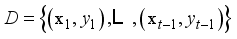 , where
, where 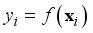 ;
; 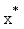 with acquisition function;
with acquisition function; 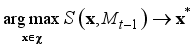 (22)
(22) 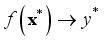 (23)
(23) 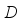 by
by 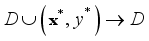 (24)
(24) 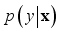 , where
, where 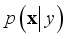 is defined as:
is defined as: 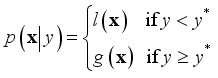 (25)
(25) 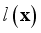 and
and 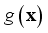 are the generation models of all domain variables, and
are the generation models of all domain variables, and 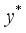 is the specific quantile. The Eq. (25) means that two different distributions are made for the parameters.
is the specific quantile. The Eq. (25) means that two different distributions are made for the parameters. 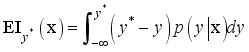 (26)
(26) 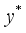 is the threshold of the objective function;
is the threshold of the objective function; 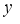 is the actual value of the objective function corresponding the parameter combination
is the actual value of the objective function corresponding the parameter combination 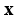 ;
; 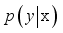 is an surrogate function expressed in probability. If the Eq. (26) is positive, it means that the parameter combination
is an surrogate function expressed in probability. If the Eq. (26) is positive, it means that the parameter combination 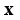 is expected to produce better results than the threshold.
is expected to produce better results than the threshold. 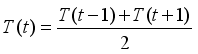 (27)
(27) Statistic | Average travel time(s) |
|---|---|
Sample size | 17480 |
Mean | 503.22 |
Standard deviation | 358.06 |
Maximum | 3782 |
Minimum | 249 |
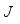 , because with the increase of decomposition scale, the loss of information is more. These two points do not have specific selection instructions, and are mostly based on experience and multiple experimental results. In this paper, db5 is selected as the basic wavelet, which is one of the commonly used wavelets in db wavelet family. It indicates that the maximum decomposition scale is 5 in the process of wavelet transform. As shown as Figure 4, when the decomposition scale is 3, the approximate component
, because with the increase of decomposition scale, the loss of information is more. These two points do not have specific selection instructions, and are mostly based on experience and multiple experimental results. In this paper, db5 is selected as the basic wavelet, which is one of the commonly used wavelets in db wavelet family. It indicates that the maximum decomposition scale is 5 in the process of wavelet transform. As shown as Figure 4, when the decomposition scale is 3, the approximate component 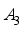 can better show the trend of the original time series. At the same time, the noise reflected in the detail component is removed, so the decomposition scale is finally selected as 3.
can better show the trend of the original time series. At the same time, the noise reflected in the detail component is removed, so the decomposition scale is finally selected as 3. 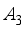 and detail component
and detail component 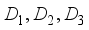 after decomposition are shown in Figure 5.
after decomposition are shown in Figure 5. 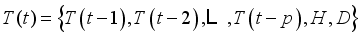 (28)
(28) 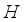 is the hourly feature and
is the hourly feature and 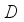 is the weekly feature, and the time lag is
is the weekly feature, and the time lag is 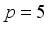 .
. 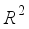 . Both MAE and RMSE can measure absolute errors between the actual and forecasting values while the MAPE is employed to evaluate the relative errors of them. The closer
. Both MAE and RMSE can measure absolute errors between the actual and forecasting values while the MAPE is employed to evaluate the relative errors of them. The closer 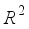 to 1, the higher the forecasting performance is. These indexes are mathematically represented as Eqs. (29) to (32):
to 1, the higher the forecasting performance is. These indexes are mathematically represented as Eqs. (29) to (32): 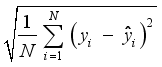 (29)
(29) 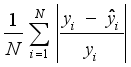 (30)
(30) 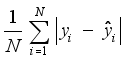 (31)
(31) 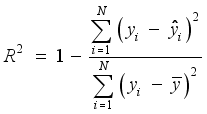 (32)
(32) 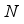 is the total number of testing data used in prediction,
is the total number of testing data used in prediction, 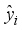 is the
is the 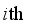 forecasting value,
forecasting value, 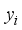 is the
is the 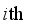 actual value, and
actual value, and 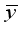 is the mean of all actual value. The forecasting results of four WDR-XGBoost sub-models are shown in Table 2.
is the mean of all actual value. The forecasting results of four WDR-XGBoost sub-models are shown in Table 2. Evaluation indexes | A3 | D3 | D2 | D1 |
|---|---|---|---|---|
RMSE | 0.0173 | 0.01 | 0.01 | 0.0141 |
MAPE | 0.1738 | 78.8512 | 180.7309 | 199.0863 |
MAE | 0.0113 | 0.0065 | 0.0077 | 0.0086 |
0.9990 | 0.9526 | 0.8844 | 0.8140 |
Evaluation indexes | SVR | XGBoost | WDR-XGBoost |
|---|---|---|---|
RMSE | 0.07791 | 0.06565 | 0.02627 |
MAPE | 0.90762 | 0.78653 | 0.30937 |
MAE | 0.05648 | 0.04837 | 0.01941 |
0.98073 | 0.98633 | 0.99781 |
WDR-XGBoost | Wavelet Decomposition and Reconstruction and the Extreme Gradient Boosting |
SVR | Support Vector Regression Model |
ARIMA | Autoregressive Integrated Moving Average model |
GARCH-M | Generalized Autoregressive Conditional Heteroscedasticity in Mean Algorithm |
LSTM | Long Short-Term Memory Neural Network |
ED | Encoder Decoder |
ConvLSTM | Convolutional LONG Short Term Memory Neural Network |
EMD | Empirical Mode Decomposition |
CNN | Convolutional Neural Network |
CWT | Continuous Wavelet Transform |
DWT | Discrete Wavelet Transform |
CART | Classification and Regression Tree |
TPE | Tree-structured Parzen Estimator |
EI | Expected Improvement Method |
RMSE | Root mean squared error |
MAPE | Mean absolute percentage error |
MAE | Mean absolute error |
| [1] | Zhao, H., Zhai, D. M., Shi, Z. H. Review of short-term traffic flow forecasting models. Urban Rapid Rail Transit. 2019, 32(4), 50-54. |
| [2] | Li, W., L, J. Z., Wang, T. Improved ARIMA model traffic flow prediction method based on box-cox exponential transformation. Journal of Wuhan University of Technology (Transportation Science & Engineering). 2020, 44(6), 974-977. |
| [3] | Zhou, T. Jiang, D. Lin, Z. et al. Hybrid dual Kalman filtering model for short-term traffic flow forecasting. IET Intelligent Transport Systems. 2019, 13(6), 1023-1032. |
| [4] | Cai, L. Zhang, Z. Yang, J. et al. A noise-immune Kalman filter for short-term traffic flow forecasting. Physica A: Statistical Mechanics and its Applications. 2019, 536, 122601. |
| [5] | Liao, R. H., Lan, S., Liu, Z. X. Short-term traffic flow forecasting based on local prediction method in chaotic time series. Computer Technology and Development. 2015, 25 (1), 1-5. |
| [6] | Hu, J. R., He, L. Freeway Traffic flow condition criterion method based on cusp catastrophe theory. China Journal of Highway and Transport. 2017, 30(10), 137-144. |
| [7] | Ma, Q. BP neural network short-term traffic flow prediction based on improved particle swarm optimization. Computer Simulation. 2019, 36(4), 94-98+323. |
| [8] | Liu, Z., Du, W., Yan, D. M., et al. Short-term traffic flow forecast based on combination of k-nearest neighbor algorithm and support vector regression. Journal of Highway and Transportation Research and Development. 2017, 34 (5), 122-128+158. |
| [9] | Yuan, H., Chen, Z. H. Short-term traffic flow prediction based on temporal convolutional networks. Journal of South China University of Technology (Natural Science Edition). 2020, 48(11), 107-113+122. |
| [10] | Fu, C. H., Yang, S. M., Zhang, Y. Promoted short-term traffic flow prediction model based on deep learning and support vector regression. Journal of Transportation Systems Engineering and Information Technology. 2019, 19(4), 130-134+148. |
| [11] | Zhang, G. Y., Jin, H. Research on the prediction of short-term passenger flow of urban rail transit based on improved ARIMA model. Computer Applications and Software. 2022, 39(1), 339-344. |
| [12] | Wang, X. Q., Shao, C., F., Yin, C., Y., et al. Short-term traffic flow forecasting method based on ARIMA-GARCH-M model. Journal of Beijing Jiaotong University. 2018, 42(4), 83-88. |
| [13] | Li, Q. R., Chi, W. Y., Chen, L., et al. Short-term traffic flow forecast based on phase space reconstruction and PSO-GPR. Journal of Transport Information and Safety. 2019, 37(2), 70-76. |
| [14] | Weng, X. X. Hao, Y. Short-term traffic flow prediction based on LSTM algorithm with the characteristics of passenger car proportion. Journal of Chongqing Jiaotong University (Natural Science). 2020, 39(11), 20-25, 50. |
| [15] | Wang, B. W., Wang, J. S., Wang, T. Y., Zhang, Z. Q., Liu Y., Yu, H. An encoder-decoder multi-step traffic flow prediction model based on long short-time memory network. Journal of Chongqing University. 2021, 44(11), 71-80. |
| [16] | Wang, Q., Li, Y., Zhang, S. T., Zhang, L. Y. Research on short-term passenger flow prediction of urban rail transit based on multilayer convolution long and short-term memory neural network. Modern Urban Transit. 2023, 9, 95-99. |
| [17] | Bui, K. N., Cho, J. Yi, H. Spatial temporal graph neural network for traffic forecasting: an overview and open research issues. Applied Intelligence. 2022, 52(3), 3763-3774. |
| [18] | Li, L., Bi, J., Yang, K., et al. MGC-GAN: multi-graph convolutional generative adversarial networks for accurate citywide traffic flow prediction. International Conference on Systems, Man, and Cybernetics. IEEE, Czech, 2022; pp. 2557-2562. |
| [19] | Aljuaydi, F., Wiwatanapataphee, B., Wu, Y. H. Multivariate machine learning-based prediction models of freeway traffic flow under non-recurrent events. Alexandria Engineering Journal. 2023, 65, 151-162. |
| [20] | Mallick, T., Balaprakash, P., Rask, E., et al. Transfer learning with graph neural networks for short-term highway traffic forecasting. The 25th International Conference on Pattern Recogintion. IEEE, Italy, 2020; pp. 10367-10374. |
| [21] | Song, X. D., Ren, M. X. The short-term traffic flow prediction based on combination model. Computer Simulation. 2022, 39(7), 156-160. |
| [22] | Teresa, P. Impact of data loss for prediction of traffic flow on an urban road using neural networks. IEEE Transactions on Intelligent Transportation Systems. 2019, 20(3), 1000-1009. |
| [23] | Zhan, H. Y., Gomes, G. Li, X. S., et al. Consensus ensemble system for traffic flow prediction. IEEE Transactions on Intelligent Transportation Systems. 2018, 19(12), 3903-3914. |
| [24] | Zheng, Z. B., Yang, Y. T., Liu, J. H., et al. Deep and embedded learning approach for traffic flow prediction in urban informatics. IEEE Transactions on Intelligent Transportation Systems. 2019, 20(10), 3927- 3939. |
| [25] | Mou, Z. H., Li, K. P., Shen, D. F. Short-term traffic flow prediction based on wavelet denoising and Bayesian neural network model. Science Technology and Engineering. 2020, 20(33), 13881-13886. |
| [26] | Liu, B., Wu, Z. D., Yang, J. Y. Research on bio-intelligence algorithm optimized wavelet neural network and its plication in traffic flow prediction. Journal of Beijing Jiaotong University. 2020, 44(5), 17-26. |
| [27] | Zhong, Y., Shao, Y. M., Wu, W. W. et al. Short-term traffic flow prediction model based on XGBoost. Science Technology and Engineering. 2019, 19(30), 337-342. |
| [28] | Ye, J., Li, L. J., Tang, Z X. Short-term traffic flow forecasting based on CNN-XGBoost. Computer Engineering and Design. 2020, 41(4), 1080-1086. |
| [29] | Antypas, E., Spanos, G., Lalas, A., Votis, K., Tzovaras, D. A time-series approach for estimated time of arrival prediction in autonomous vehicles. Transportation Research Procedia. 2024, 78, 166-173. |
| [30] | Chen, B. Y., Chen, X. Y., Chen, H. P., Huang, Y. B., Jia, T., Lam. W. H. Understanding user equilibrium states of road networks: Evidence from two Chinese mega-cities using taxi trajectory mining. Transportation Research Part A: Policy and Practice. 2024, 180(1), 103976. |
APA Style
Wang, X., Fang, F. (2024). Short-Term Traffic Flow Prediction Based on Wavelet Analysis and XGBoost. International Journal of Transportation Engineering and Technology, 10(1), 15-24. https://doi.org/10.11648/j.ijtet.20241001.12
ACS Style
Wang, X.; Fang, F. Short-Term Traffic Flow Prediction Based on Wavelet Analysis and XGBoost. Int. J. Transp. Eng. Technol. 2024, 10(1), 15-24. doi: 10.11648/j.ijtet.20241001.12
AMA Style
Wang X, Fang F. Short-Term Traffic Flow Prediction Based on Wavelet Analysis and XGBoost. Int J Transp Eng Technol. 2024;10(1):15-24. doi: 10.11648/j.ijtet.20241001.12
@article{10.11648/j.ijtet.20241001.12,
author = {Xin Wang and Fang Fang},
title = {Short-Term Traffic Flow Prediction Based on Wavelet Analysis and XGBoost
},
journal = {International Journal of Transportation Engineering and Technology},
volume = {10},
number = {1},
pages = {15-24},
doi = {10.11648/j.ijtet.20241001.12},
url = {https://doi.org/10.11648/j.ijtet.20241001.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ijtet.20241001.12},
abstract = {Traffic flow prediction is of great significance for urban planning and alleviating traffic congestion. Due to the randomness and high volatility of urban road network short-term traffic flow, it is difficult for a single model to accurately estimate traffic flow and travel time. In order to obtain more ideal prediction accuracy, a combined prediction model based on wavelet decomposition and reconstruction (WDR) and the extreme gradient boosting (XGBoost) model is developed in this paper. Firstly, the Mallat algorithm is applied to perform multi-scale wavelet decomposition on the average travel time series of the original traffic data, and single branch reconstruction is performed on the components at each scale. Secondly, XGBoost is used to predict each reconstructed single-branch sequence, so as to obtain multiple sub-models, and the Bayesian algorithm is used to optimize the hyperparameters of the sub-models. Finally, the algebraic sum of the predicted values of all sub-models is used to obtain the overall traffic prediction result. To test the performance of the proposed model, actual traffic flow data has been collected from a certain link of the Brooklyn area in New York, USA. The performance of proposed WDR-XGBoost model has been compared with other existing machine learning models, e.g., support vector regression model (SVR) and single XGBoost model. Experimental findings demonstrated that the proposed WDR-XGBoost model performs better on multiple evaluation indicators and has significantly outperformed the other models in terms of accuracy and stability.
},
year = {2024}
}
TY - JOUR T1 - Short-Term Traffic Flow Prediction Based on Wavelet Analysis and XGBoost AU - Xin Wang AU - Fang Fang Y1 - 2024/07/23 PY - 2024 N1 - https://doi.org/10.11648/j.ijtet.20241001.12 DO - 10.11648/j.ijtet.20241001.12 T2 - International Journal of Transportation Engineering and Technology JF - International Journal of Transportation Engineering and Technology JO - International Journal of Transportation Engineering and Technology SP - 15 EP - 24 PB - Science Publishing Group SN - 2575-1751 UR - https://doi.org/10.11648/j.ijtet.20241001.12 AB - Traffic flow prediction is of great significance for urban planning and alleviating traffic congestion. Due to the randomness and high volatility of urban road network short-term traffic flow, it is difficult for a single model to accurately estimate traffic flow and travel time. In order to obtain more ideal prediction accuracy, a combined prediction model based on wavelet decomposition and reconstruction (WDR) and the extreme gradient boosting (XGBoost) model is developed in this paper. Firstly, the Mallat algorithm is applied to perform multi-scale wavelet decomposition on the average travel time series of the original traffic data, and single branch reconstruction is performed on the components at each scale. Secondly, XGBoost is used to predict each reconstructed single-branch sequence, so as to obtain multiple sub-models, and the Bayesian algorithm is used to optimize the hyperparameters of the sub-models. Finally, the algebraic sum of the predicted values of all sub-models is used to obtain the overall traffic prediction result. To test the performance of the proposed model, actual traffic flow data has been collected from a certain link of the Brooklyn area in New York, USA. The performance of proposed WDR-XGBoost model has been compared with other existing machine learning models, e.g., support vector regression model (SVR) and single XGBoost model. Experimental findings demonstrated that the proposed WDR-XGBoost model performs better on multiple evaluation indicators and has significantly outperformed the other models in terms of accuracy and stability. VL - 10 IS - 1 ER -